House prices in 'S72 0', Great Houghton
Price per square metre data and charts revealed. Latest statistics for the housing market in 'S72 0' (Great Houghton, Cudworth) - calculated on 04 February 2026.
Defining 'S72 0'
This analysis is limited to properties whose postcode starts with "S72 0", this is also called the postcode sector. There are no official postcode sector names so I've just labelled it S72 0, Great Houghton. It is shown in red on the map below.
Want to change geography?
You can click on the map above to change to a neighbouring sector, or you can use the search form below.
Price per square metre
Knowing the average house price in S72 0 is not much use. However, knowing average price per square metre can be quite useful. Price per sqm allows some comparison between properties of different size. We define price per square metre as the sold price divided by the internal area of a property:
£ per sqm = price ÷ internal area
For example in December 2025, 8, Byron Street, Great Houghton, S72 0ED sold for £200,000. Given the internal area of 76 square metres recorded on the EPC, the price per sqm is £200,000 ÷ 76 sqm = £2,631.
England & Wales have been officially metric since 1965. However house price per square foot is prefered by some estate agents and those of sufficiently advanced age ;-). You can change your prefered units from square meters to square feet for all the graphs and charts on S72 0 and elsewhere. Just visit the My Account page and look for the m2 to ft2 toggle switch. Alternatively just multiply everything by 10, move a decimal place to go from sqm to sqft and you'll be close enough as 1 sqm = 10.76391 sqft.
Distribution of £ per sqm for 'S72 0' vs 'S72'
The chart above is called a histogram, it helps you see the distribution of house price per sqm in S72 0 To make this chart we put all the sales data into a series of £ per sqm 'buckets' (e.g. £2,350 to £2,500, £2,500 to £2,650, £2,650 to £2,800 etc...) we then count the number of sales with within in each bucket and plot the results. The histogram is based on 87 sales that took place in S72 0, Great Houghton, Cudworth in the last 24 months.
Generate a custom histogram like the one above but based on your own criteria.
You can see the spread of prices above. This is because although internal area is a key factor in determining valuation, it is not the only factor. Many factors other than size affect desirability; these factors could be condition, aspect, garden size, negotiating power of the vendor etc.
The spread of prices will give you a feel of the typical range to expect in S72 0, Great Houghton. Notably, only 25% of properties that sold recently were valued at more than £2,200 sqm. For anything to be valued more than this means it has to be more desireable than the clear majority of S72 0 homes.
Box plot of £ per sqm for S72 0
Tip: click on the chart to see the values.
The chart above is called a boxplot (or a box-and-whisker plot). Box plots, like histograms, are used to graphically represent the distribution of data, showing the central tendency, spread of the distribution. In the context of £ per square metre property price distributions, box plots represent the variation in property prices within a geographic area e.g. Great Houghton. The chart above shows a boxplot for 'S72 0' as well as the 'S72' postcode district.
Property price map for Great Houghton
Have a look at the interactive price map I created for myself. Use it to explore 'S72 0' house prices all the way down to individual property plots.
Great Houghton house price forecasting
House prices in S72 0 fell -2.9% in the last year, -6.5% after inflation. Whether or not this trend will continue depends on many factors, such as wage growth, net migration, interest rates and the level of house building. No one can predict these things with certainty however we can plot the historic trends in house prices in S72 0 (Great Houghton) compared with the wider postcode district of S72.
House price index for S72 0
Tip: click on the legend items to show/hide different lines
Download house price index as CSV (premium users only).
The chart above shows changes in 'S72 0' property prices over the last 20 years. The index is calculated from the average price paid per sqm for property in S72 0 and is set to 100 in 2004. I'm comparing the trends for S72 0,Great Houghton with the wider postcode district of S72 What is more interesting is to look at the difference between flats and houses, even those in the same area follow a very different trend, to get a robust enough sample size to see this we need to zoom out and look at house price trends for the entire local authority.
The dashed lines show nominal house price changes, the solid lines show the same data adjusted for inflation. Economists call this the 'real' price change. You have to take inflation into account when comparing prices over time. It's calculated using the formula:
Real Rate of Return = (1 + Nominal Rate) ÷ (1 + Inflation Rate) – 1In this formula, the nominal rate is the rate of change before any adjustments, and the inflation rate is taken from the Consumer Price Index. The real rate of return is a more accurate measure of change in value, because £1 today does not have the same buying power as £1 in the past. For example, if a savings account pays an interest rate of 3% per year and the inflation rate is 5% per year, the real rate of return is -2%. This means that the investment's value is shrinking by 2% each year.
Historic returns for S72 0
| S72 0 sector | S72 district | |||
|---|---|---|---|---|
| Nominal | Real | Nominal | Real | |
| 20 yr per annum | 2.3% | -0.5% | 2.6% | -0.2% |
| 20 yr total | 57.6% | -8.7% | 66.6% | -3.4% |
| 10 yr per annum | 4.7% | 1.5% | 5.3% | 2.1% |
| 10 yr total | 58.2% | 16.2% | 67.5% | 23.0% |
| 5 yr per annum | 6.3% | 1.7% | 7.3% | 2.6% |
| 5 yr total | 35.5% | 8.6% | 42.2% | 14.0% |
| 1 yr per annum | -2.9% | -6.5% | 6.3% | 2.3% |
| 1 yr total | -2.9% | -6.5% | 6.3% | 2.3% |
This table complements the house price index chart above, presenting the data in a more detailed format. It breaks down the information into 20-year, 10-year, 5-year, and 1-year periods, further categorized by property type. For each period, we display both a per annum rate of change and a total rate of change.
The total rate of change represents the overall change over the entire period. The formula for total return is:
Total return = (Index at end of period ÷ Index at start of period) - 1
The per annum rate of change is the annualized rate of change over the period. This is equivalent to the annual bank savings rate you would need to achieve the same total return over the given period. This annualized return is also known as the Compound Annual Growth Rate (CAGR). The formula for CAGR is:
CAGR = (1 + Total return) ^ (1 ÷ Number of years) - 1
Some specific examples:
- Over the past 20 years, S72 district have seen a -0.2% annual change when adjusted for inflation. This translates to a total change of -3.4% in real terms.
- Over the past 5 years, S72 0 sector have seen a 1.7% annual change when adjusted for inflation. This translates to a total change of 8.6% in real terms.
Most recent S72 0 sales
For the most recent sales activity, rather than a summarized average, it is better to see the underlying data. This is shown in the chart below, where blue dots represent individual sales, click on them to see details. If there is an obvious trend you should be able to spot it here amid the noise from outliers.
Tip: hover over dots to see details
Street level data
| Street | Avg size | Avg £sqm | Recent sales |
|---|---|---|---|
| High Street, Great Houghton, S72 0A | 107 sqm | £2,001 | 8 |
| Norfolk Road, Great Houghton, S72 0D | 82 sqm | £1,781 | 8 |
| Pleasant Avenue, Great Houghton, S72 0B | 86 sqm | £1,502 | 6 |
| Middlecliff Lane, Great Houghton, S72 0H | 95 sqm | £1,713 | 6 |
| School Street, Great Houghton, S72 0A | 89 sqm | £1,365 | 5 |
| Windsor Crescent, Great Houghton, S72 0H | 77 sqm | £1,383 | 5 |
| Thurnscoe Lane, Great Houghton, S72 0D | 99 sqm | £2,207 | 5 |
| Normandale Road, Great Houghton, S72 0A | 88 sqm | £1,242 | 5 |
Search for your street here.
Nearby geographies
The table below shows how 'S72 0' compares to the other postcode sectors in S72.
| Sector | Lower quartile | Median | Upper quartile | Sales in last 2yr |
|---|---|---|---|---|
| S73 9 Darfield | £1,330 sqm | £1,880 sqm | £2,390 sqm | 174 |
| S73 0 Wombwell | £1,470 sqm | £1,990 sqm | £2,630 sqm | 406 |
| S72 9 Brierley | £1,740 sqm | £2,070 sqm | £2,760 sqm | 109 |
| S72 8 Cudworth | £1,490 sqm | £2,050 sqm | £2,630 sqm | 405 |
| S72 7 Grimethorpe | £1,460 sqm | £1,780 sqm | £2,210 sqm | 152 |
| S72 0 Great Houghton | £1,250 sqm | £1,750 sqm | £2,200 sqm | 87 |
| S71 5 Ardsley | £1,670 sqm | £2,230 sqm | £2,640 sqm | 217 |
| S63 9 Goldthorpe | £690 sqm | £1,200 sqm | £2,130 sqm | 350 |
| S63 8 Bolton Upon Dearne | £1,140 sqm | £1,450 sqm | £2,010 sqm | 235 |
| S63 7 Wath Upon Dearne | £1,570 sqm | £2,090 sqm | £2,700 sqm | 249 |
Raw data
Our analysis of S72 0 is derived from what is essentially a big table of sold prices from Land Registry with added property size information. Below are three rows from this table to give you an idea.
| Address | Paid | sqm | £/sqm |
|---|---|---|---|
| 8, Byron St, Great Houghton, Cudworth | £200,000
Dec-2025
|
76 | 2,631 |
| 44, Rotherham Rd, Great Houghton, Cudworth | £130,000
Dec-2025
|
64 | 2,031 |
| 85, Manor Fields, Great Houghton, Cudworth | £260,000
Nov-2025
|
114 | 2,280 |
About
I created HouseMetric because I wanted to see this data and analysis myself, I also wanted to teach myself to build a website. Please give me feedback or spread the word about it. I'm constantly tinkering and adding more stuff to it.
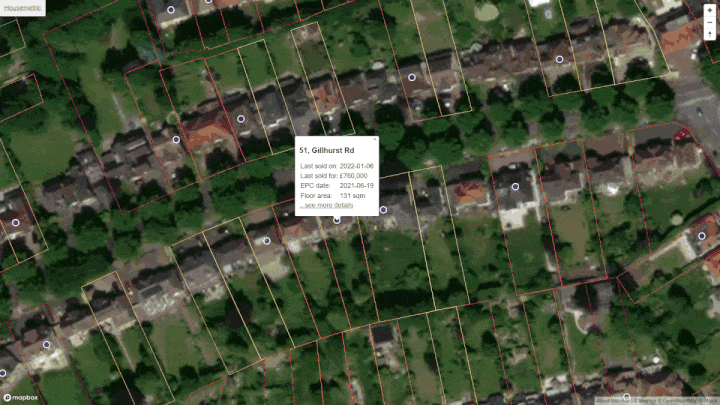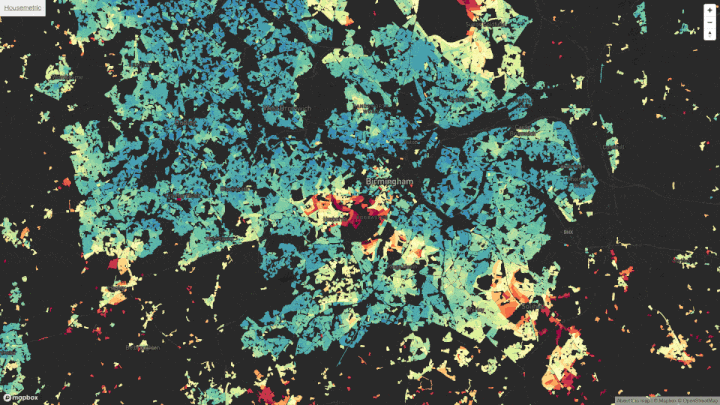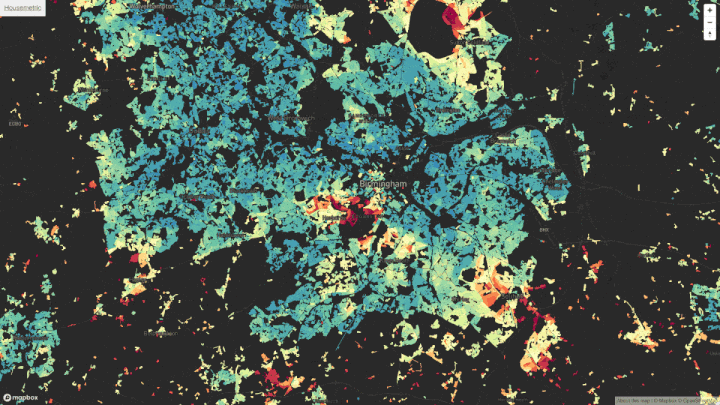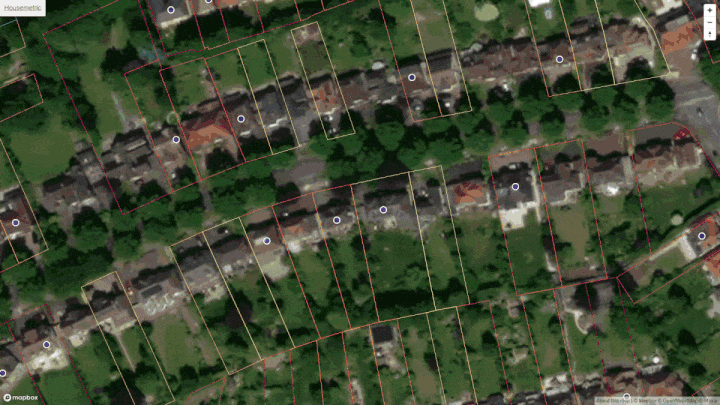 House price map for Great Houghton
House price map for Great Houghton